1651. Максимальный XOR

Задан набор целых чисел a₁, a₂, ..., a_n. Для заданного числа x найдите такое a_i, что x xor a_i максимально.

Вход. Первая строка содержит количество чисел n (n ≤ 10⁵) и количество запросов q. Вторая строка содержит целые числа a₁, a₂, ..., a_n (0 ≤ a_i ≤ 10¹⁸). Каждая из следующих q строк содержит одно число x (0 ≤ x ≤ 10¹⁸).

Выход. Для каждого значения x выведите в отдельной строке такое значение a_i, для которого x xor a_i максимально.

Пример входа	Пример выхода
5 6 5 3 7 2 6 1 2 4 5 3 6	6 5 3 2 5 3

РЕШЕНИЕ

бор

Анализ алгоритма

Занесем все входные числа a₁, a₂, ..., a_n в бинарный бор. Каждая вершина бора имеет два сына, которые соответствуют битам 0 и 1. Поскольку a_i ≤ 10¹⁸, 2⁶⁰ > 10¹⁸, то каждое a_i содержит не более 61 бита (которые нумеруются от 0 до 60).

Теперь покажем как для заданного x найти такое a_i, что x xor a_i максимально. Пусть x = b₁b₂…b_n – двоичное представление числа. Если существует такое i что a_i = (через обозначен инвертированный бит b_k), то двоичное представление x xor a_i будет состоять из n единиц и является наибольшим из возможных. Двигаемся по бору последовательно по битам . Если для некоторого k в боре пути по биту нет, то двигаемся по биту b_k. В конце прохода по битам x прийдем в вершину, которой соответствует искомое a_i.

Пример

Числа во входном примере содержат не более 3 бит. Построим бинарный бор, где каждое число представлено тремя битами.

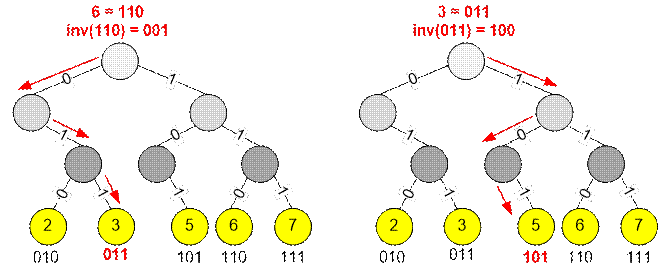
Пусть x = 6 = 110₂. Инвертируем биты: inv(110₂) = 001₂. Двигаемся по бору:

· первый шаг: бит 0 в боре есть;

· второй шаг: бита 0 в боре нет, двигаемся по 1;

· третий шаг: бит 1 в боре есть;

Мы пришли к числу a_i = 3.

Реализация алгоритма

Объявим бинарный бор trie. В переменной TrieSize храним его размер.

#define MAX 60 * 100000

int trie[MAX][2];

int TrieSize;

Пусть все биты числа a_i вставлены в бор. Если число a_i заканчивается в вершине номер v бора, то установим num[v] = a_i. Таким образом для любой вершины бора мы будем знать, конечная ли она для некоторого a_i, и если ответ утвердительный, то сможем получить и само значение a_i.

long long num[MAX];

Функция Insert вставляет число x в бор. Биты вставляем в порядке от старшего к младшему.

void Insert(long long x)

{

int i, v = 0;

for (i = 60; i >= 0; i--)

{

Извлекаем i-ый бит числа x в переменную bit.

int bit = x & (1LL << i) ? 1 : 0;

Если пути по биту bit в боре нет, то создаем новую вершину.

if (trie[v][bit] == -1)

trie[v][bit] = TrieSize++;

Двигаемся по бору дальше.

v = trie[v][bit];

}

Вершина v – конечная для числа x. Сохраним эту информацию.

num[v] = x;

}

Функция Find(x) возвращает такое a_i, для которого x xor a_i максимально.

long long Find(long long x)

{

int i, v = 0;

for (i = 60; i >= 0; i--)

{

Двигаемся по бору по битам, реверсным к двоичному представлению числа x.

int bit = x & (1LL << i) ? 0 : 1; // reverese bit

Если движение по бору невозможно, двигаемся по другому биту.

if (trie[v][bit] == -1) bit ^= 1;

v = trie[v][bit];

}

Возвращаем значение a_i, соответствующее вершине бора v.

return num[v];

}

Основная часть программы. Читаем входные данные. Изначально бор содержит одну вершину (TrieSize = 1).

scanf("%d %d", &n, &q);

TrieSize = 1;

memset(trie, -1, sizeof(trie));

memset(num, -1, sizeof(num));

Вставляем числа входной последовательности a₁, a₂, ..., a_n в бинарный бор.

for (i = 0;i < n; i++)

{

scanf("%lld", &x);

Insert(x);

}

Обрабатываем q запросов. Для каждого входного значения x ищем такое значение a_i, что x xor a_i максимально.

for (i = 0;i < q; i++)

{

scanf("%lld", &x);

x = Find(x);

printf("%lld\n", x);

}